Research at RERI: Higher-order Reservoir Simulation
Our research in reservoir simulation focuses on algorithms that include unstructured grids,
have low numerical dispersion, and have high accuracy. We are interested in multiphase, multicomponent
flow in fractured and in heterogeneous media. The combination of mixed finite elements, and
discontinuous Galerkin method have features compatible with problems of interest to us. Due to the
increased interest in CO2 injection, phase behavior modeling is an integral part of our reservoir
simulation. In the compositional modeling we are interested to guarantee the global minimum of Gibbs
free energy. Thermodynamic stability analysis is used to help with the global minimum free energy.
There has been much progress in our higher-order reservoir modeling and in our immiscible
multiphase flow. Some of the results from our modeling work are shown in the following. Current
work includes devising new algorithms that can speed up computations by orders of magnitude through
fundamental physics and new mathematical formulations.
Numerical Dispersion by Finite Difference (FD) and Discontineous Galerkin (DG) Methods |
|
Hoteit, H., and Firoozabadi, A.: "Compositional Modeling by the Combined Discontinuous Galerkin and Mixed Methods," SPE J (2006) 11(1), 19-34.
There is a vast difference between the numerical errors in first-order finite difference (FD) and discontinuous Galerkin (DG) methods for the same mesh size. In 2D, the computational speed in about two orders higher in our DG compared to first-order finite difference schemes for compositional flows. |
|
Mikyška, J., and Firoozabadi, A.: "Implementation of Higher-Order Methods for Robust and Efficient Compositional Simulation," J Comput Phys (2010) 229, 2898–2913.
|
|
| Gas Saturation (fraction) | CO2 composition (mole fraction) |
|
To take advantage of the powerful features of higher-order methods, we sometimes need to formulate our basic equations in accordance with the numerical scheme. With the appropriate formulation the code runs robustly as seen above from the CO2 injection from the bottom. |
|
|
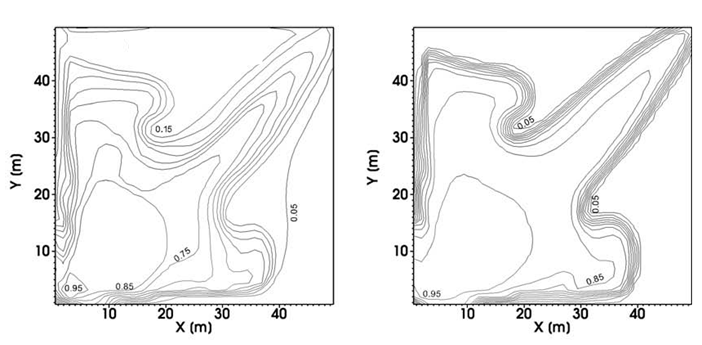
Hoteit, H., and Firoozabadi, A.: "Numerical Modeling of Two-Phase
Flow in Heterogeneous Permeable Media with Different Capillarity Pressures,"
Adv Water Resour (2008) 31, 56-73.
Capillary pressure contrast between the layers can sharpen the front in layered media. Without the capillary pressure or when an average capillary pressure is used, the results on the left are obtained. |
|
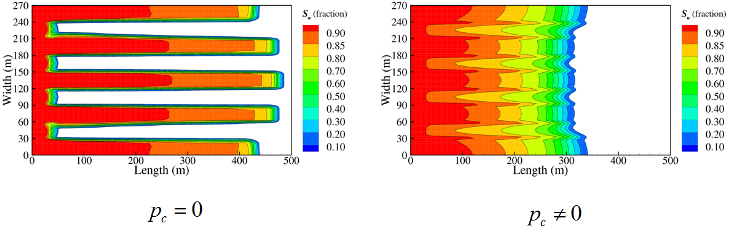
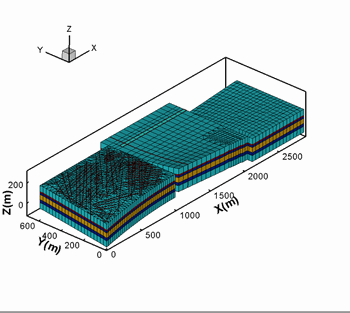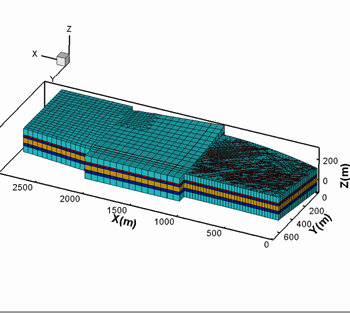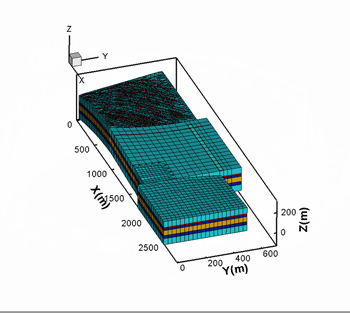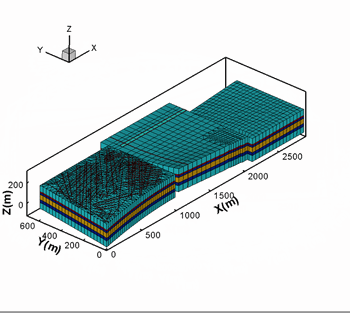
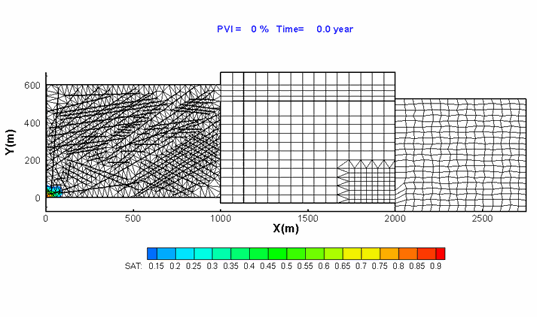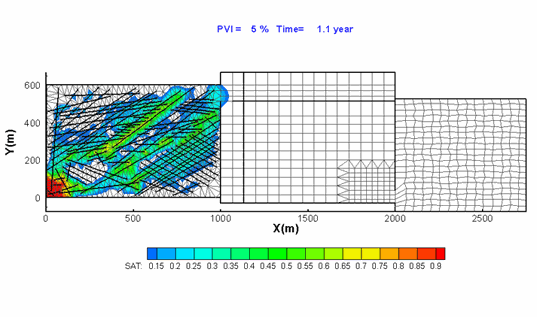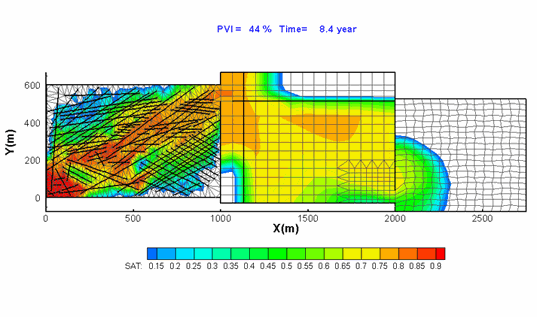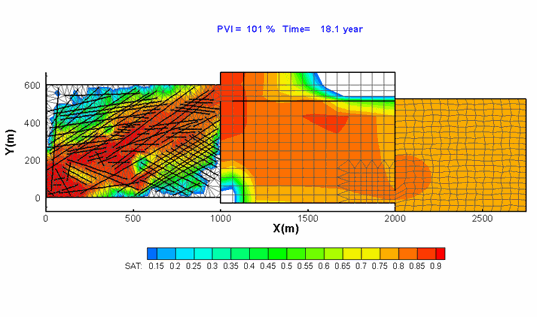
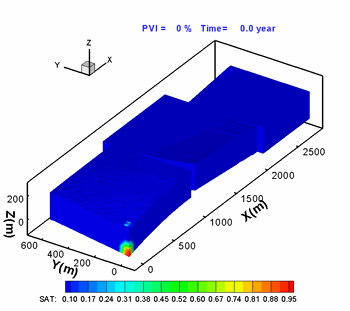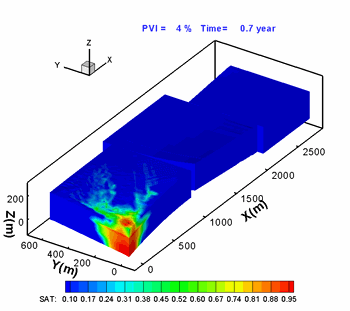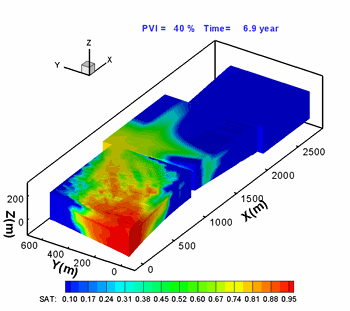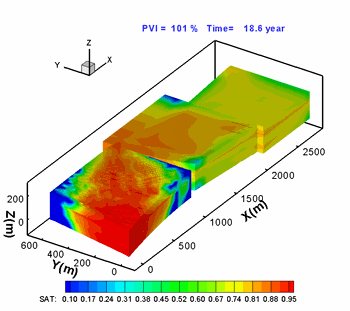
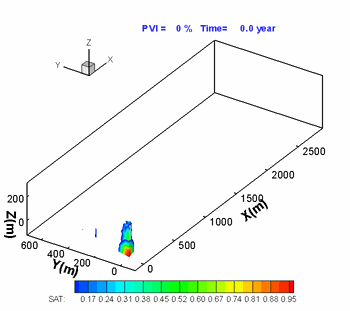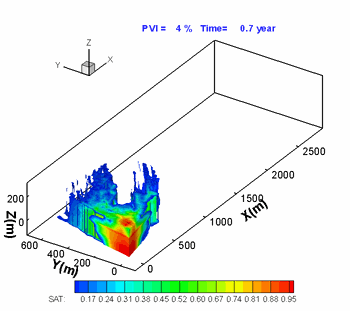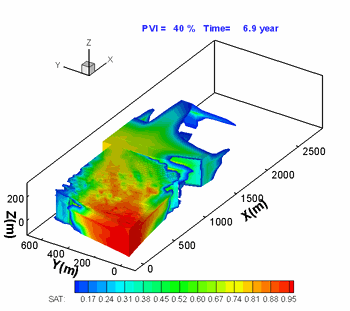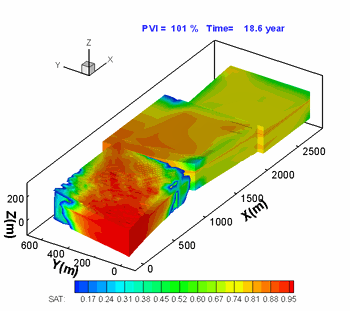
Hoteit, H., and Firoozabadi, A.: "An Efficient Numerical Model for Incompressible Two-Phase Flow in Fractured Media," Adv Water Resour (2008) 31, 891-905 a) Gridding
Unstructured gridding with any quality is a requirement for accurate modeling of flow in descrete fractured porous media. Our higher-order method provides accurate modeling of species flow and velocity fields in complex fractured media. b) Flow Paths
Water injection in such a complex fractured media can only be performed with a higher-order method if accurate results are desired. |
|
|
c) Flow Paths in Matrix |
d) Flow Path in Fractures |
|
|
|
|
3D geometry and fractured complexity create challenges that can only be addressed by using a comprehensive numerical scheme. |
Flow in the fractures (shown above) is coupled with matrix flow. |
|
Moortgat, J., Li, Z. and Firoozabadi, A.: "Three-Phase Compositional
Modeling of CO2 Injection by Higher-Order Finite Element Methods with PR and CPA Equations of
State," Water Resour Res (2012) 48, W12511:
|
|
|
Viscous fingering during WAG injection in anisotropic 600 m by 60 m domain saturated with oil and 30% connate water. The vertical permeability is 50 times lower than the 221 md horizontal permeability. Alternating slugs of 2.5% pore volume of water and 2.5% slugs of gas are injected uniformly from the left boundary, and production is at constant pressure from the right. The gas is 80 mol% CO2 and 20mol% methane and has a density similar to the oil in the reservoirs, but a much lower viscosity. Because of the high viscosity ratio, pronounced viscous fingers develop. These fingers are easily resolved by our higher-order finite element methods, while they are often suppressed by numerical dispersion when traditional finite difference methods are used. Mixtures of the injected gas and the 9-(pseudo)component oil are near the critical point, which makes the three-phase compositional modeling and phase behavior computations challenging. |
|
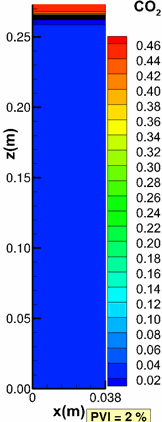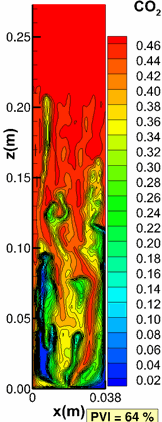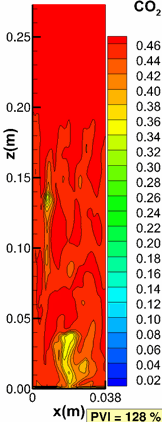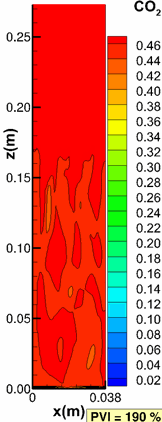
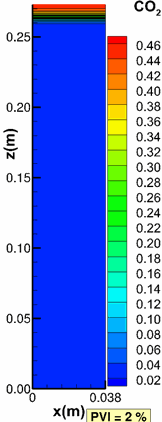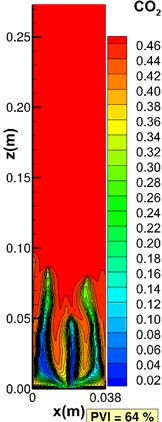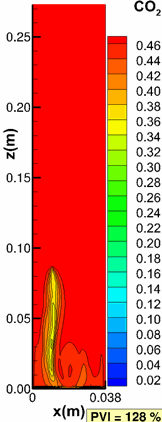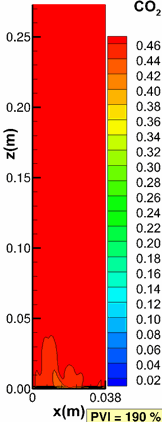
Moortgat, J., Firoozabadi, A., Li, Z. and Esposito, R.: "CO2 Injection in Vertical and Horizontal Cores: Measurements and Numerical Simulation," SPE J (2013), 18(2), 331-344. |
|
|
|
|
|
|
|
|
Moortgat, J., Li, Z. and Firoozabadi, A.: "Three-Phase Compositional Modeling of CO2 Injection by Higher-Order Finite Element Methods with PR and CPA Equations of State," Water Resour Res (2012) 48, W12511. |
|

|

|
| Formation permeability is 1 darcy, 5% PV injected in 33.3yr | Formation permeability is 100 mili-darcy, 5% PV injected in 500yr |
|
|
|
|
Moortgat, J., and Firoozabadi, A.: "Three-Phase Compositional Modeling with Capillarity in Heterogeneous and Fractured Media," SPE J (2013), 18(6), 1150-1168. |
a) 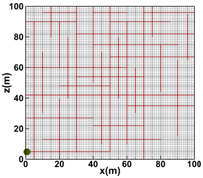 b)
b) 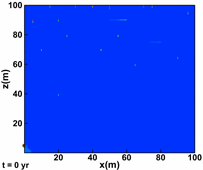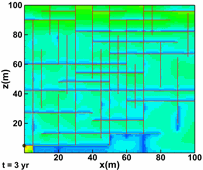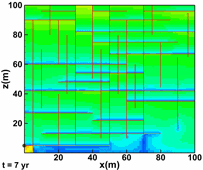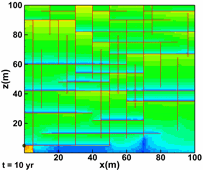 c)
c) 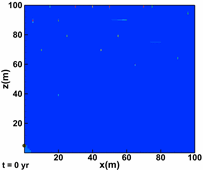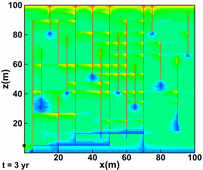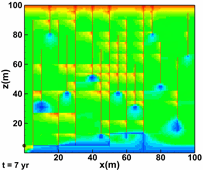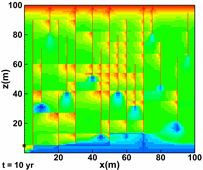

|
|
|
.png)